在物理学中,我们通常使用两种基本的力学理论来描述自然界的行为:量子力学和经典力学。
这两种理论在许多情况下都能够提供准确的描述,但当我们涉及到复杂的多体系统时,情况变得更加复杂。
在这些情况下,通常需要从量子力学转换到经典力学,以便进行更简单和可行的计算。
这一尺度转换问题一直是物理学家们的焦点,吸引了广泛的研究兴趣。
在过去的几十年里,研究人员已经提出了各种方法来解决这一问题,例如半经典方法、准经典方法和WKB近似等。
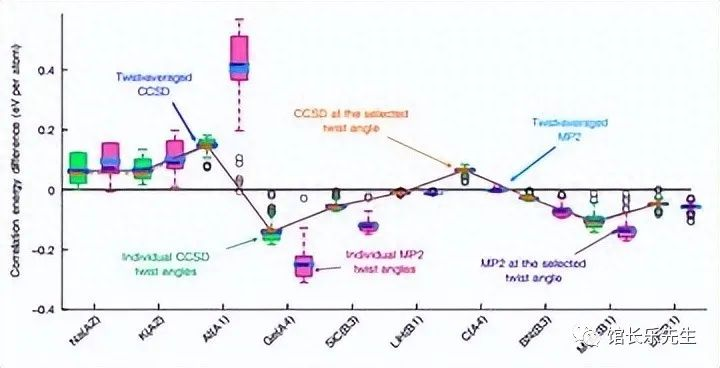
尽管这些方法在某些情况下取得了成功,但它们仍然存在一些局限性。
因此,我们需要一种新的视角来更深入地理解从量子多体系统到经典力学的尺度转换过程。
本论文将提出一种新的量子-经典对应原理的视角,该原理旨在为这一尺度转换提供更清晰的理论基础。
我们将从传统的哈密顿动力学和路径积分方法出发,逐步展示如何将量子多体系统转化为经典力学框架,并讨论其在不同尺度下的适用性。
同时,我们还将探讨这一新视角对量子多体系统研究的潜在影响以及未来研究方向。
量子力学和经典力学的基本原理
第一定律(惯性定律),物体将保持匀速直线运动,或保持静止,除非有外力作用于它。
第二定律(运动定律),物体的加速度与作用在其上的力成正比,与物体的质量成反比,可以用F=ma表示。
第三定律(作用与反作用定律):作用在物体上的力总是会有一个等大小但方向相反的反作用力。
经典力学假设宏观物体的状态(位置、速度、质量等)可以精确测量,并且它们的轨迹可以预测。
在经典力学中,如果我们知道系统的初始条件和外部力,就可以精确地预测未来的系统行为。
这意味着系统的演化是确定性的。

量子力学中,粒子既具有粒子性质也具有波动性质。
这意味着粒子的位置和动量不能同时完全确定,存在一种不确定性。
由于波粒二象性,根据海森堡不确定性原理,我们无法同时精确测量一个粒子的位置和动量。
精确定位粒子将导致动量的不确定性,反之亦然。
量子系统的状态由波函数(或量子态矢量)来描述,通常用Ψ表示。
波函数包含了有关粒子的所有信息,但我们只能通过测量来获取有关粒子状态的信息。
根据量子叠加原理,一个量子系统可以同时处于多个可能的状态的线性组合,直到测量时才会坍缩到其中一个状态。

量子系统的演化由薛定谔方程来描述。
这个方程指导着波函数随时间的演化,从而决定了粒子的行为。
量子力学允许不同粒子之间存在纠缠,即使它们之间有很远的距离。
这种纠缠导致了一些奇特的现象,如Einstein-Podolsky-Rosen (EPR) 悖论。
总之,经典力学和量子力学在描述物质和能量的行为时采用了截然不同的原理。
经典力学适用于宏观物体的运动,其演化是确定性的,而量子力学适用于微观粒子的行为,其中存在不确定性和波粒二象性。
这两个理论在不同尺度和条件下都具有其独特的适用性。

量子多体系统中的尺度效应
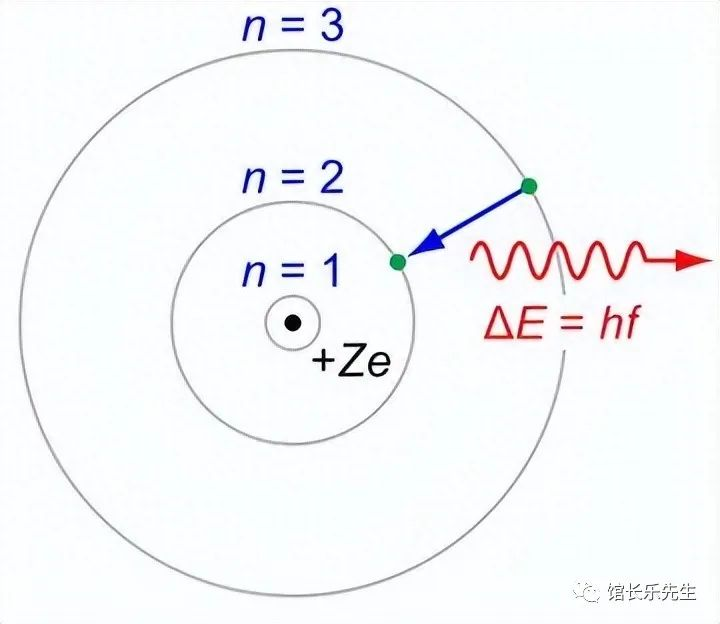
在量子力学中,存在一种特定的长度尺度,称为康普顿波长(Compton wavelength),它与粒子的动量相关。
康普顿波长决定了在该尺度下,粒子的波动性质开始显现,而不再可以被视为经典点粒子。
在小于康普顿波长的尺度下,粒子的位置和动量不再能够同时精确测量。
在量子多体系统中,不同粒子之间的相互作用会导致量子相干性的出现。
这是一种尺度效应,其中粒子之间的量子纠缠关系在相对较短的距离上仍然存在。
随着距离的增加,相互作用逐渐减小,粒子之间的纠缠也减弱,系统的行为趋于经典。
在微观尺度下,粒子可以通过隧道效应穿越经典禁阻势垒,而不需要具备足够的能量。
这一效应在纳米尺度的电子器件和化学反应中起着关键作用,因为它使得一些看似经典禁阻的过程在量子水平上仍然可能发生。
在小尺度下,量子系统的涨落效应变得显著。
这意味着物理量(如能量或粒子数)不再保持恒定,而是随时间波动。
这些涨落可以导致一系列微观现象,如量子热力学效应和零点振荡。
在多体量子系统中,尺度效应与量子纠缠密切相关。
在临界点附近,小尺度的量子纠缠可以引发量子相变,其中系统的基态发生显著变化。这些相变通常伴随着量子涨落的增强。
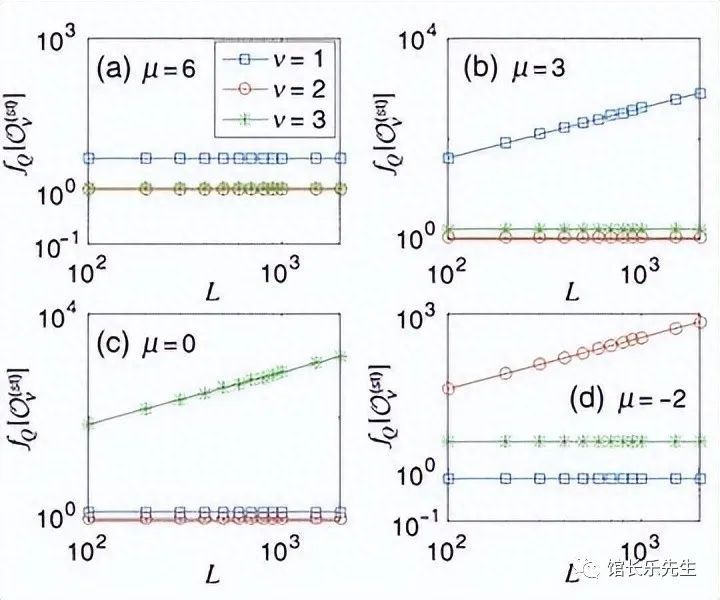
在大尺度下,量子多体系统的行为逐渐接近经典热力学的极限。
在高温下或者在密度较低的情况下,系统的量子效应通常变得可以忽略,而系统的行为可以用经典热力学来描述。
总之,量子多体系统中的尺度效应是由于系统的大小、相互作用强度和温度等因素的变化而导致的,这些效应在不同尺度下可以产生不同的量子和经典行为。
理解和控制这些尺度效应对于研究和应用量子多体系统非常重要,尤其在纳米科学、量子信息科学和凝聚态物理等领域。
传统方法的局限性
传统方法通常局限于处理特定类型的势能或简单的系统。
它们在描述高度非线性的势能、高维度系统或者存在强相互作用的系统时效果不佳。
这些方法难以处理复杂的量子多体系统,如凝聚态物理系统中的电子-电子相互作用。
在一些情况下,传统方法难以提供清晰的经典轨迹,因为它们主要集中在波函数的相位信息上。
经典轨迹对于直观理解系统的行为非常重要,但这些方法未能提供足够的信息。
传统方法通常忽视了量子多体系统中的纠缠效应,而这些效应在系统的尺度转换中起着关键作用。
纠缠效应可以导致非经典的行为,例如量子隧道效应和量子涨落。
传统方法有时需要进行复杂的数学计算,尤其是在处理高维度系统或复杂势能表面时。
这可能导致计算的困难性和计算资源的需求增加。
传统方法通常依赖于系统处于平衡态或近平衡态,而在非平衡态下,这些方法的适用性有限。
这限制了对一些重要的物理现象(如量子输运)的理解。
对于时间演化问题,传统方法有时需要复杂的数值时间演化方法,这些方法在处理长时间尺度上可能会变得非常耗时。

综上所述,传统方法在处理量子多体系统到经典力学的尺度转换问题时存在一些明显的局限性。
为了克服这些局限性,一些新的方法和工具,如基于纠缠熵的方法或量子-经典对应原理的新视角,已经被提出,以更全面和准确地描述这些尺度转换问题。
这些新方法在理论和计算上提供了更强大的工具,以更好地理解复杂多体量子系统的行为。
基于纠缠熵的新方法
纠缠熵是一种度量量子系统中纠缠程度的物理量。
它衡量了一个子系统与其余系统之间的相互依赖程度。
高纠缠熵表示子系统之间高度纠缠,低纠缠熵表示子系统之间几乎没有纠缠。
通常,对于一个由多个粒子组成的量子多体系统,可以定义各种子系统,如子空间或者不同位置的粒子。
纠缠熵用来描述这些子系统之间的关联程度。
基于纠缠熵的方法通过观察系统中的纠缠熵随时间的演化来识别量子多体系统何时趋向于经典极限。
当纠缠熵迅速减小并达到某个阈值时,系统的行为可以被视为经典的。
这个阈值通常与系统的尺度和温度有关。在高温和大尺度下,经典极限通常更容易达到。

一旦纠缠熵降低到足够低的水平,基于纠缠熵的方法可以用来导出经典力学中的Hamiltonian,从而描述系统的经典行为。
这种过渡通常涉及将量子运动方程(薛定谔方程)转化为经典运动方程(Hamiltonian方程),并且可以用来模拟系统的经典轨迹。
基于纠缠熵的方法相对较适用于各种多体量子系统,包括凝聚态物理、量子信息科学和量子化学等领域。
它特别有用于描述量子相变或量子-经典的连续过渡。
基于纠缠熵的方法的挑战之一是处理大规模系统的计算复杂性。
对于大型多体系统,计算其纠缠熵可能变得非常昂贵。此外,该方法的有效性通常取决于如何选择系统的子系统,以及如何定义和测量纠缠熵。

结语
在量子多体系统中,尺度转换是一个关键问题,涉及将量子行为过渡到经典行为的描述和理解。
传统方法,如WKB近似和路径积分方法,虽然在某些情况下有用,但它们存在一些明显的局限性。
基于纠缠熵的新方法提供了一种更全面的视角,使我们能够更好地理解和描述这一尺度转换过程。
通过监测系统中的纠缠熵,基于纠缠熵的方法允许我们识别量子多体系统何时趋向于经典极限。

当系统的纠缠熵降低到足够低的水平时,系统的行为可以被视为经典的,从而允许我们导出经典力学中的描述。
这一方法的优势在于它适用于各种多体量子系统,并提供了一种更直观的方式来理解尺度转换。
然而,基于纠缠熵的方法也存在一些挑战,包括计算复杂性和如何选择合适的子系统等。
因此,这个领域仍然需要进一步的研究和发展。

总的来说,基于纠缠熵的方法为我们提供了一种全新的视角,用于研究量子多体系统中的尺度效应和尺度转换问题。
这一方法有望在理论物理学、凝聚态物理学和量子信息科学等领域产生重要影响,为我们更深入地理解和探索量子世界提供了新的工具和理论框架。
通过不断改进和扩展这些方法,我们可以更好地解释和利用量子多体系统的奇特性质,推动科学和技术的发展。